 管制图的研读及判别并非只是观察其样本点有否超出管制界线这么简单。
管制图的研读及判别并非只是观察其样本点有否超出管制界线这么简单。
其实管制图的判读应该要以机率的「检定」方法来鑑别其有否「非机遇原因」发生,而管制图的最主要目的就是为了要抓出这种「非机遇原因」并即时的加以管制。
既使所生产之品质特性其真实结果并不是常态分佈,但透过抽样的管制图描画的结果仍然会呈现出常态分佈图。所以参考上图的常态分佈图说明1~3个标准差(σ)的机率大小,就会发现样本点的分佈应该会有如下的特性:
-
样本点的分佈呈常态随机状态,无任何规则可循。
-
多数样本点集中在中心线附近。
-
少数样本点落在上、下管制界限附近。
-
应该没有样本点会超出管制界限。(机率非常小,只有0.27%=2700ppm)
所以举凡所抽取的样本点刚好有好几个全部都落在管制中心的同一侧(因为机率很低),或连续几个样本点都没有落在一个标准差以内,或是连续多个样本点全都集中在一个标准差内…等这些违反机率理论的抽样点分佈,都可能是非机遇原因所造成,也就需要依照人、工、料、机、量、环等手法来检查制程条件是否发生了异常,然后加以排除。
下面是一些常见的管制图判别之方法,请将之对照最前面的常态分佈图的机率大小,就可以知道为何这样的样本点分佈会被认为有问题而必须加以处理:
管制图样本点分佈之研读及判异准则
- 一样本点或多样本点落在三倍标准差管制界限外。(α=0.0027)
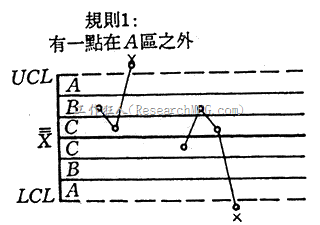
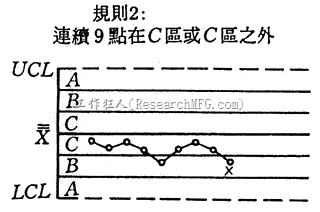
- 连续9样本点落在中心线同一侧。(α=0.0038)
- 连续11样本点中有10样本点落在中心线同一侧。
- 连续14样本点中有12样本点落在中心线同一侧。
- 连续17样本点中有14样本点落在中心线同一侧。
- 连续20样本点中有16样本点落在中心线同一侧。
- 连续6样本点持续上升或下降。(α=0.00237)

- 连续14样本点之相邻点刚好一上一下交替。(α=0.0027)

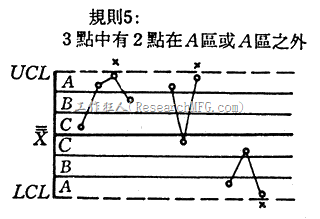
- 连续的3样本中有2样本点落在两倍标准差警告界限外,但还在管制界限内。 (α=0.00268)
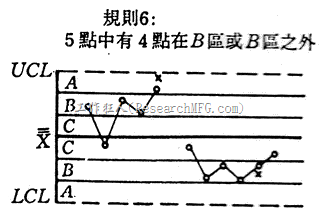
- 连续的5样本点中有4样本点落在距离中心线上、下一倍标准差外。 (α=0.0021)
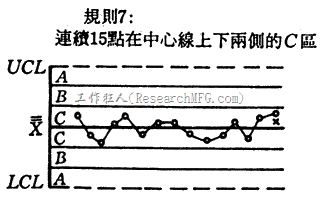
- 15样本点落在中心线上下一倍标准差内。(表示抽样有问题) (α=0.00326)
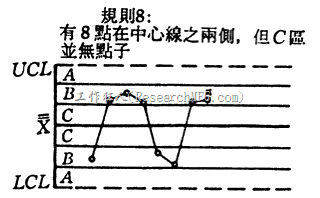
- 连续8样本点没有任何一样本点落在中心线上、下一倍标准差内。 (α=0.0002)
- 资料出现任何有系统性变化的非随机图形的型态。
- 一样本点或多样本点落在警告界限或管制界限附近。
ISO 8258:1991 管制图样本点分佈判稳准则
- 抽样到一个样本点未出界,不能立即判稳,但若连续管制界限内有更多点出现时,既使有个别样本点偶然出界,制程仍可看做是稳态的。
- 在样本点随机排列的情况下,符合下述情形则判稳:
- 连续25点,落于界外的点 d=0 (α1=0.0654)
- 连续35点,落界外的点 d≤1 (α2=0.0041)
- 连续100点,落界外的点 d≤2 (α3=0.0026)
延伸阅读:
柏拉图分析 (Pareto Chart)介绍
标准差与常态分佈的关系(six sigma)
制程能力介绍 ─ Cpk之制程能力解释
六个标准差(six sigma)运用于日常生活
如何使用Excel2007建立常态分布曲线图表
如何使用Excel2007制作柏拉图(Pareto chart)
品管七大工具-管制图绘制及建立的步骤与方法
贊助商广告


PayPal
欧付宝









你好,想请问你的每一个a值是怎么计算出来的,谢谢
Reply